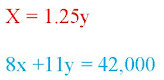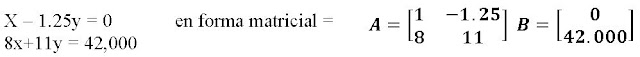EJEMPLOS DE APLICACIÓN DE MATRICES DENTRO DE LA VIDA PROFECIONAL Y/O COTIDIANA

 

MATRICES

El Álgebra lineal son un conjunto bidimensional de números o símbolos distribuidos de forma rectangular, en líneas verticales y horizontales, de manera que sus elementos se organizan en filas y columnas.

Para mas detalles mire el video;

APLICACIONES

Las matrices pueden ser aplicadas tanto en la vida cotidiana como en la laboral.

Ya que abarcan casi todos los problemas comúnmente visto en el diario vivir, como el sacar cuentas de una empresa, hasta la cantidad de dinero que gasta una persona al hacer varias compras a la vez.

A continuación compartiremos aplicaciones graguitas para facilitar la realización de ejercicios en donde se aplican matrices y ecuaciones de primer grado.

Geogebra, Photomaht, Matrix Calculator

A continuación veremos ejemplos con su desarrollo donde se aplican las matrices para solucionar los problemas o necesidades que se pueden encontrar a diario.

EJEMPLO 1

Las matrices A, B y C corresponden a la información, en miles de bolivianos, para los 3 primeros meses del año de las ventas, costos y utilidades (columnas) mensuales para dos empresas (filas) de una misma corporación.

Encontrar el valor de las ventas, costos y utilidades para el primer trimestre del año.

Dentro de este ejemplo solo hay que ejecutar una simple suma de matrices que se desarrolla de la siguiente manera:

EJEMPLO 2

Un local tiene 100 revistas, 70 libros de cocina y 90 novelas en existencia.
El valor de cada revista es de 28 bs, cada libro de cocina cuesta 22 bs y cada novela 16 bs.

Determinar el inventario total a través del producto de matrices.

Para resolver este problema primero debemos agrupar el inventario en una matriz fila:

El costo de cada producto lo agrupamos como un vector columna de la siguiente manera:

Para determinar el valor del inventario lo que debemos hacer es simplemente multiplicar ambas matrices de tal manera que nos dé un producto de matrices de la siguiente manera:

Luego de hacer una multiplicación de matrices, tenemos nuestro resultado final:

EJEMPLO 3

La fábrica de fragancias Julio César posee tres marcas X,Y y Z, distribuyendo su producción en cuatro tiendas los litros almacenados en la primera tienda vienen dados por la siguiente matriz:

Si la segunda tienda almacena el doble que la primera, la tercera la mitad y la cuarta el triple ¿Qué volumen de producción se tiene almacenado en total­?

Lo que buscamos se puede obtener resolviendo la siguiente operación:

Si intercambiamos la matriz A en la operación nos quedaría lo siguiente:

Luego de haber hecho las multiplicaciones por los respectivos escalares para cada matriz, nos queda que el resultado es:

EJEMPLO 4

La fábrica EDMUNDO elabora dos tipos de sábanas (A y B). Por cada unidad que vende A, la ganancia es de 8 Bs y por cada unidad de B la ganancia es de 11 Bs.
Para el año siguiente la fábrica desea una ganancia total de 42,000 Bs

La experiencia les indica que puede venderse un 25% más de A que de B.

 ¿Cuántas unidades de cada uno debe vender?

X será el numero de unidades de A y Y las unidades de B.
Con los datos del problema se plantean las siguientes ecuaciones:

Si el producto A se vende 25% mas que B entonces planteamos que:

Entonces resolvemos las ecuaciones una vez interpretadas:

Para resolver la ecuación debemos hallar la inversa de la matriz A:

Por lo tanto, para hallar X y Y debemos multiplicar la Matriz inversa de A por la matriz B entonces tenemos que:

Y el resultado sería el siguiente:

Por lo que para alcanzar la ganancia esperada, la compañía EDMUNDO debe vender 2500 unidades de el producto A y 2000 unidades del producto B.